Modeling in the Geosciences

Numerical models are a novel tool used to predict changes, visualize processes, and identify relationships for the advance of scientific research. Models combine a culmination of years of scientific research in physics, statistics, and data collection into one place where scenarios can be interpreted and predicted. As with much of research within the geosciences, modelers have to reconcile with uncertainty and assumptions as they try to simplify the complexities of the real world into a comprehensible result. A modeler’s goal is not necessarily to recreate the exact reality of the geological world, but rather better define the bounds of what is possible or not possible in terms of processes, time, and scale to produce an observable phenomenon within data or physics.

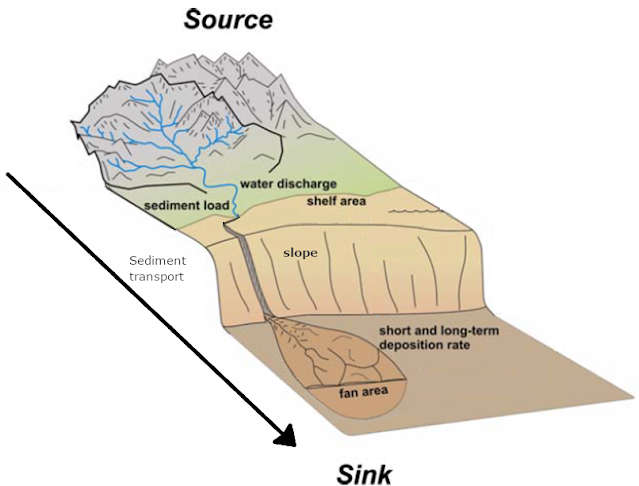
In the Geosciences, one type of tool and field of study are Landscape Evolution Models (or LEMs). They are used to recreate processes at the surface. Based on physical equations, it is possible to look at the evolution of hillslopes, erosion, weathering, river incision, and sediment transport mechanisms. Time is of great importance, and different LEMs use different timescales from years to millions of years depending on the processes being modeled.

One model used within our studies of sediment routing systems from source to sink is a landscape evolution model called Fastscape (Bovy, 2021; Braun and Willet, 2013). Fastscape uses different modifications of the stream power law to simulate drainage, erosion, deposition, and topographic elevation of a landscape over geologic time. As an example, in figure 1 we show how Fastscape can be used to visualize the changes within topography and landscape response to changes in bedrock erodibility.


Figure 1: Sample Fastscape Landscape Evolution Model Set Up

Using Fastscape, geoscientists can assess the response of a catchment (drainage divide migration, erosion rates, channel dynamics, etc) to changes in precipitation, uplift, flexural subsidence and more. This is useful when trying to recreate external forcing events within the stratigraphic record, calculate sediment budgets, or analyze response times of a catchment. Fastscape has also been used to derive analytical solutions for landscape controls on fan extent and slope (Braun, 2022) based on geometries observable across different model simulations. Modeling is a constantly evolving scientific field and thus, updates and improvements of models are regularly made. For example, as part of our project, we develop new codes to add to Fastscape, incorporating new tools to the system.

The modeling world and incorporation of models by geoscientists is ever expanding and thus, we cannot even begin to summarize it within one blog post. Overall, the potential uses of a model go so far as the bounds of scientific inquiry-i.e essentially limitless.



References

Bovy, B. (2021). Fastscape-lem/fastscape: Release v0.1beta3 (0.1.0beta3). Zenodo: https://doi.org/10.5281/zenodo.4435110

Braun, J., & Willett, S. D. (2013). A very efficient O (n), implicit and parallel method to solve the stream power equation governing fluvial incision and landscape evolution. Geomorphology, 180, 170-179.

Braun, J. (2022). Comparing the transport-limited and ξ–q models for sediment transport. Earth Surface Dynamics, 10(2), 301-327.




Comments

Post a Comment

Popular posts from this blog

What is a Source-to-Sink System?

Image
A  source-to-sink analysis is a method in sedimentary geology that integrates the studies of an entire sedimentary system from its upstream source in the continental area to the ultimate depositional sink , most commonly on deep basin s, in a process that can take from thousands to millions of years to be completed.   Source-to-sink system schematic (modified from Martinsen et al., 2010). There are three main elements in the source-to-sink system, source, transfer zone, and sink.       1) Source Source area in the source-to-sink system is in the continental realm where the main erosional processes occur. The erosion process in the source area is mainly driven by slow processes which can take millions of years: tectonics and climate. Tectonics generates high relief structures like mountains while climatic factors like precipitation bring water down the mountains. Hence, more sediment supply can be provided from the source area.  During the erosion pro...
Read more

What is a “Slow” Process in a Source-to-Sink System?

Image
The timescale of geological processes is very extensive. “Fast” processes like earthquakes, storms, or tides last from a couple of minutes to weeks. “Slow” processes, like orogenic uplifts or continent break-ups on the contrary can take up to millions of years (Fig. 1). In this post we will look into these slow processes in the context of the source-to-sink approach, introducing some concepts that provide a useful framework to understand the dynamics of these long processes in sedimentary systems. Figure 1. Temporal scale showing the differences in terms of duration of several geological processes as well as the common tools used to measure them. Bear in mind that the scale is logarithmic. Modified from Romans et al ., 2016. To understand slow geological processes in the context of source-to-sink analysis, we first have to understand the concept of steady-state topography. There are two major processes that drive topography inside a catchment (Fig. 2), one that creates positive rel...
Read more

ITN opportunities: Summer-schools (Part 1)

Image
Since the beginning of the project, multiple interesting opportunities have been presented to us. We would travel each year to conferences like EGU, present and convene, introduce ourselves to the scientific community, make connections, go on different secondments according to our needs during our doctoral studies, but also opportunities to meet each other during the years, with one important meeting for everyone each year: the summer schools. It was the only time where all of us were together for multiple weeks, to exchange, learn and evolve in our respective fields, but also learn in more detail about the subjects of our colleagues. Some cooperation started between us thanks to those summer schools. To cite some, Marine and Philémon during Dragonstone, in Spain in 2021 or Amanda, Rocío, Nahin, Ariel and Marine during Inside Africa, in Namibia in 2023. Thus, it is appropriate to present, through this blog, an overview about the summer schools. We could talk about each of them for da...
Read more